Definition of the Radial Distribution Function

Radial distribution functions (also called RDFs or g(r)) are a metric of local structure, making them ideal for characterizing amorphous materials that, by definition, lack long-range order and therefore produce no strong diffraction peaks.

Calculating a radial distribution function is conceptually very simple. You first choose an atom around which the RDF will be calculated. For every value of r, construct a spherical shell of radius r and width dr centered on your chosen atom, then calculate the density (e.g., in atoms per cubic centimeter) within that spherical shell:

Graphical depiction of how the RDF is calculated

In the 2d representation pictured,

g(r) = 12 atoms / (2 pi r dr)

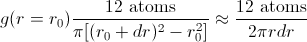
RDFs usually represent the time- and position-averaged result of this calculation; that is, the RDF around every single atom is calculated, averaged together, and then this is repeated over many different points in time to get a statistically meaningful representation of the system’s short-range structure.

Because the volume of each shell increases as r increases,

lim(r to infinity) g(r) = nmol / (xl yl zl)

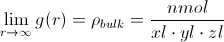
It is very common to express g(r) as a normalized radial distribution function, where the radial distribution function is simply divided by this bulk density at all points. Furthermore, it is computationally trivial to decompose the RDF into contributions from different pairs (e.g., the radial distribution of Si around O centers). These pair-specific RDFs are technically known as “pair distribution functions” (PDFs) or “pair correlation functions” (PCFs).

Experimentally, g(r) can be derived from scattering spectra (such as x-ray diffraction, neutron scattering, or electron diffraction) via Fourier transforms. As such, it is possible to compare the results of our simulations directly to experimental data using radial distribution functions.

Using rdfshg

There are a number of different analysis codes we use that produce RDFs from knite1 files. rdfshg is one of the more versatile versions as it reports information on the coordination of atoms in addition to producing g(r). To use it, you must have the input file, called rdflist, in the same directory as the knite1 and knite9 you wish to analyze. It is annotated with what parameters belong on each line, and here is a brief explanation of each variable:

  • the first and second lines are the filenames of the knite9 and knite1 to be analyzed
  • iread is the number of saves to read out of the knite1
  • ijump is the sampling interval; e.g., ijump = 3 reads every third save up to the ireadth save
  • iskip is how many saves to skip from the beginning of the knite1
  • iatom is the ltype of the central atom for the RDF (e.g., the solid black atom in the RDF schematic above)
  • jatom is the ltype of the neighbors to examine (e.g., the grey atoms in the RDF schematic)
  • iall = 0 ignores iatom and jatom and calculates a true RDF over all atoms; iall = 1 uses iatom and jatom to calculate a PDF
  • istart, istop specify the range for iatom. This is useful for heterogeneous systems; for example if istill = 1000, you should exclude these from the RDF by setting istart = 1000. Setting istart = istop = 0 is the same as istart = 1 and istop = nmol.
  • jstart, jstop are analogous to istart and istop. Following the example above, if istill = 1000 but jstart = 0 the resulting g(r) will exclude frozen atom centers (black atom schematic) but can include frozen neighbors (grey atoms in schematic).
  • rcut short nn is the first-neighbor cutoff distance for bonds between atoms of type iatom and jatom. For example, if iatom = 1 (Si) and jatom = 2 (O), our standard rcut short is 2.0 Å. This parameter is used to calculate the coordination number of iatom.
  • rcut long nn is the cutoff distance for second-nearest neighbor atoms and is used to calculate the second-nearest neighbor coordination number.
  • rc is how far out you want g(r) to go. 10.0 Å is a standard distance.
  • zlow and zhi are the minimum and maximum z value over which g(r) should be calculated. This serves a purpose not unlike istart/istop/jstart/jstop and is useful in calculating RDFs near interfaces in heterogeneous systems. Note that zhi does not actually do anything in many versions of rdfshg.
  • lcoord specifies the central ltype for the coordination number calculation. This should be the same as iatom.
  • ipbc = 1 if your simulation used periodic boundary conditions; = 0 otherwise. This will usually be 1.
  • isurf should be the same as isurf from your tape5
  • iltype toggles between using ltypes and using lt, which is an alternative identifier for atoms. This will usually be 1.
  • izuse determines whether to use zlow and zhi to restrict the RDF calculation. Note that this does not actually work in many versions of rdfshg.
  • ismooth is a parameter for the smoothing algorithm to reduce noise in the RDF. ismooth = 0 presents the raw RDF data without any smoothing; ismooth > 0 (e.g., 1, 2, etc.) applies increasingly aggressive data smoothing.
  • nbin is the number of data points to use in g(r) for 0 < r < rc. Increasing nbin increases data resolution, but it too many bins causes significant noise in g(r).

Once rdflist is properly configured, run rdfshg, bearing in mind that it may have a slightly modified name (e.g., rdfshg.x or rdfshg2.x). It will generate a few output files. Speak with whomever gave you your rdfshg code for the most accurate information, but here are some common outputs:

  • r1 simply contains the x values for g(r)
  • rdf1 contains the y values for the three-dimensional g(r)
  • rgr contains x and y values for g(r) (i.e., r1 and rdf1 combined)
  • rdf2 contains y values for the two-dimensional g(r)

Plotting the Data

You can skim the numerical output of rdfshg, but it may be easier to either paste the contents of the output into a spreadsheet and plot it that way or use gnuplot.

Mean Coordination

Radial distribution functions can be used to derive a number of important quantities from a system. A very simple manipulation of the RDF will give you the mean coordination number for a specific type of atom j around a central atom i. Recalling that

derivation step 1
derivation step 2

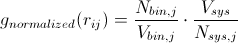
At this point it should be easy to envision this analytically rather than numerically; that is, at infinitely small bin widths,

derivation step 3

Or, if we integrate between two local minima,

derivation step 4

Converting dV to dr is quite straightforward:

derivation step 5
derivation step 6
derivation step 7

which gives us

derivation step 8

or

derivation step 9

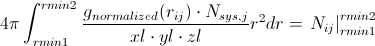
Going back to our calculated g(r), we can then evaluate the left side of the above equation numerically to get the average number of atoms of type j around a central atom of type i at interatomic spacings rmin1 < rij < rmin2. If the first peak in the RDF is bounded by rmin1 and rmin2, you get the average number of nearest neighbors. This can be extended to the second peak, which would yield the second-nearest-neighbors. This can be a very useful metric in determining the defect concentration in glasses, ionic coordination in solutions, etc.

You can get a sense for how this RDF calculation is performed by looking at an example RDF calculation I implemented in Python.

Next page: Extracting Data from Output with grep