This page contains information about training LLMs using reduced precision.
Variants
- FP8 - either E5M2 or E4M3
- MXFP8 - either E5M2 or E4M3
- NVFP4 - NVIDIA’s implementation of
Hardware
- H100 supports FP8, but not MXFP8. This means that handling high dynamic range within a tensor must be done in software when training in 8-bit precision.
- B200 supports
- MXFP8 in hardware, allowing tensors to be divided up into consecutive blocks of 32 values with different scaling factors. The dynamic range within a block is constrained, but different blocks within a tensor can have high dynamic range.
- FP4 (E2M1), but the scaling factor must be handled entirely in software
- MXFP4 (E2M1) with 32-value blocks
- NVFP4 (E2M1) with 16-value blocks
Examples
- DeepSeek-R1 was trained using fine-grained quantization (see FP8 training); by NVIDIA’s estimation, this gave only a 38% speedup over training in BF16.
- Llama-3.1 was trained using bfloat16
Training in FP8
Info
The following is taken from my GTC25 blog.
The most eye-opening talk I attended about the realities of low-precision arithmetic was “Stable and Scalable FP8 Deep Learning Training on Blackwell.” Contrary to my naïve prior assumption, you can’t just cast every model weight from BF16 to FP8 and expect training to just work. Rather, training in such low precision requires figuring out all the places across a neural network where you can get away with low precision, then carefully watching the model as you train to make sure that low precision doesn’t wreck your results.
More specifically, training with low precision requires dividing up the entire neural network into regions that are safe to compute with FP16, regions that are safe to compute with FP8, and regions (like softmax) which unsafe for both FP8 and FP16. Scaling factors are used to prevent underflow or overflow of FP8/FP16 by multiplying contiguous regions of low-precision values by a power-of-two constant as they are being computed. One scaling factor is used for an entire low-precision region though, so you can get in trouble if the values within a low-precision range have too much dynamic range—if a tensor cast as FP8 has values that vary by many orders of magnitude, the likelihood of underflow or overflow when applying a scaling factor to that tensor becomes high.
Figuring out how to partition every tensor in a deeply multi-layer language model into safe regions with low dynamic range—and making sure these partitions don’t diverge into an unstably high dynamic range as the model trains—is a gnarly problem. To make this easier, NVIDIA ships their Transformer Engine library which implements various “recipes” that safely cast tensors down to FP8 using different strategies, like applying one scaling factor to an entire tensor, to each row, or to finer-grained “sub-channels” (parts of rows or parts of columns).
Hopper GPUs do not support fine-grained scaling factor blocks for FP8 in hardware, so benchmarking these different “recipes” on H100 reveals a wide variety of speedups compared to training in 16-bit precision:
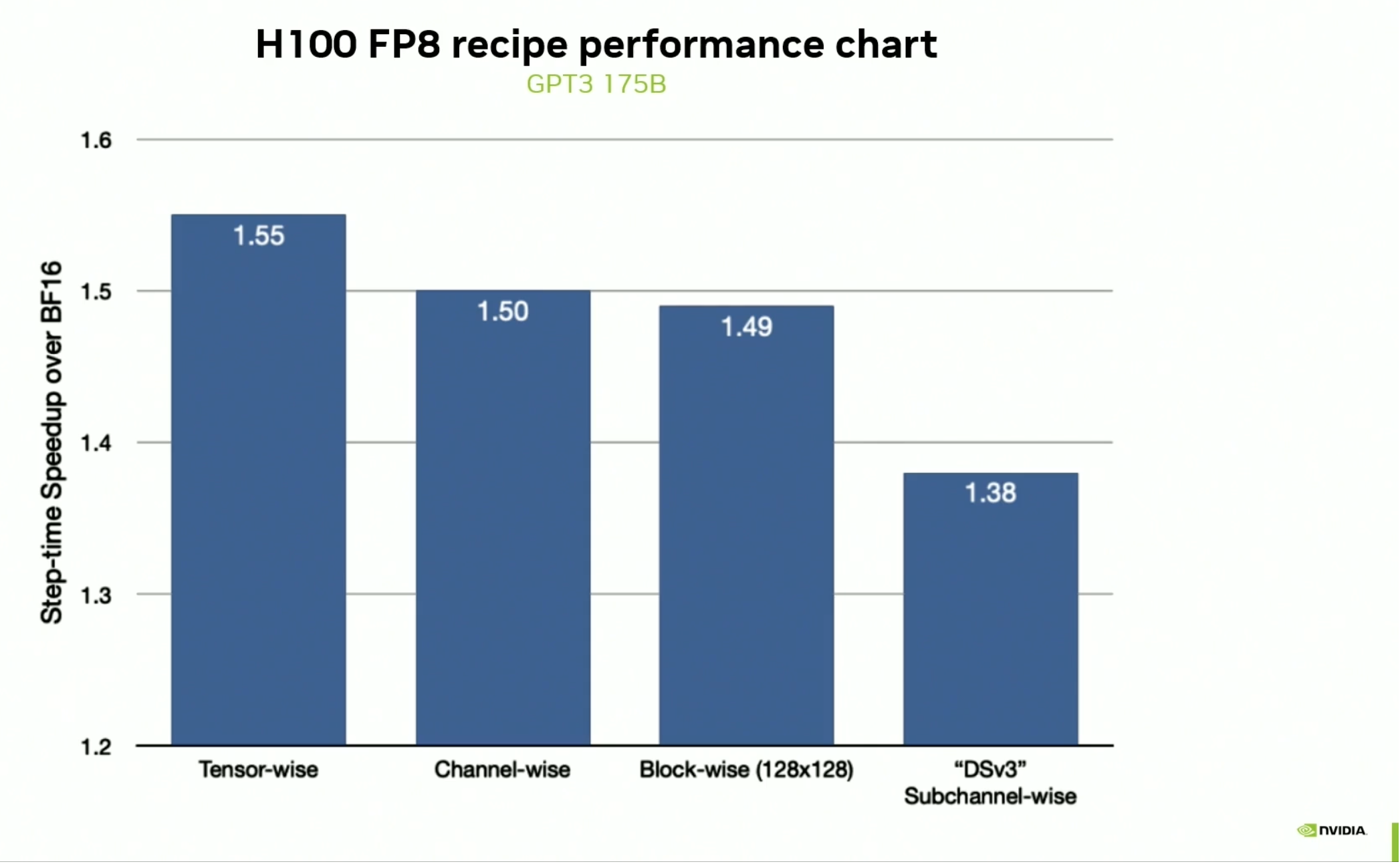
Despite the fact that Hopper has 2x the peak FP8 FLOPS than BF16 FLOPS on its spec sheet, the above results show that you don’t get nearly 2x performance when training using FP8. Furthermore, the sub-channel partitioning recipe used to train Deepseek (DSv3) yields the worst overall speedup because the fine-grained use of scaling factors had to be implemented inside the matrix multiplication loop by repeatedly multiplying these sub-channel blocks by their respective scaling factors.
This presentation went on to show that Blackwell closes this gap by introducing hardware support for microscaled FP8 (MXFP8), a format in which blocks of 32 values (either in a row or column) share one scaling factor:
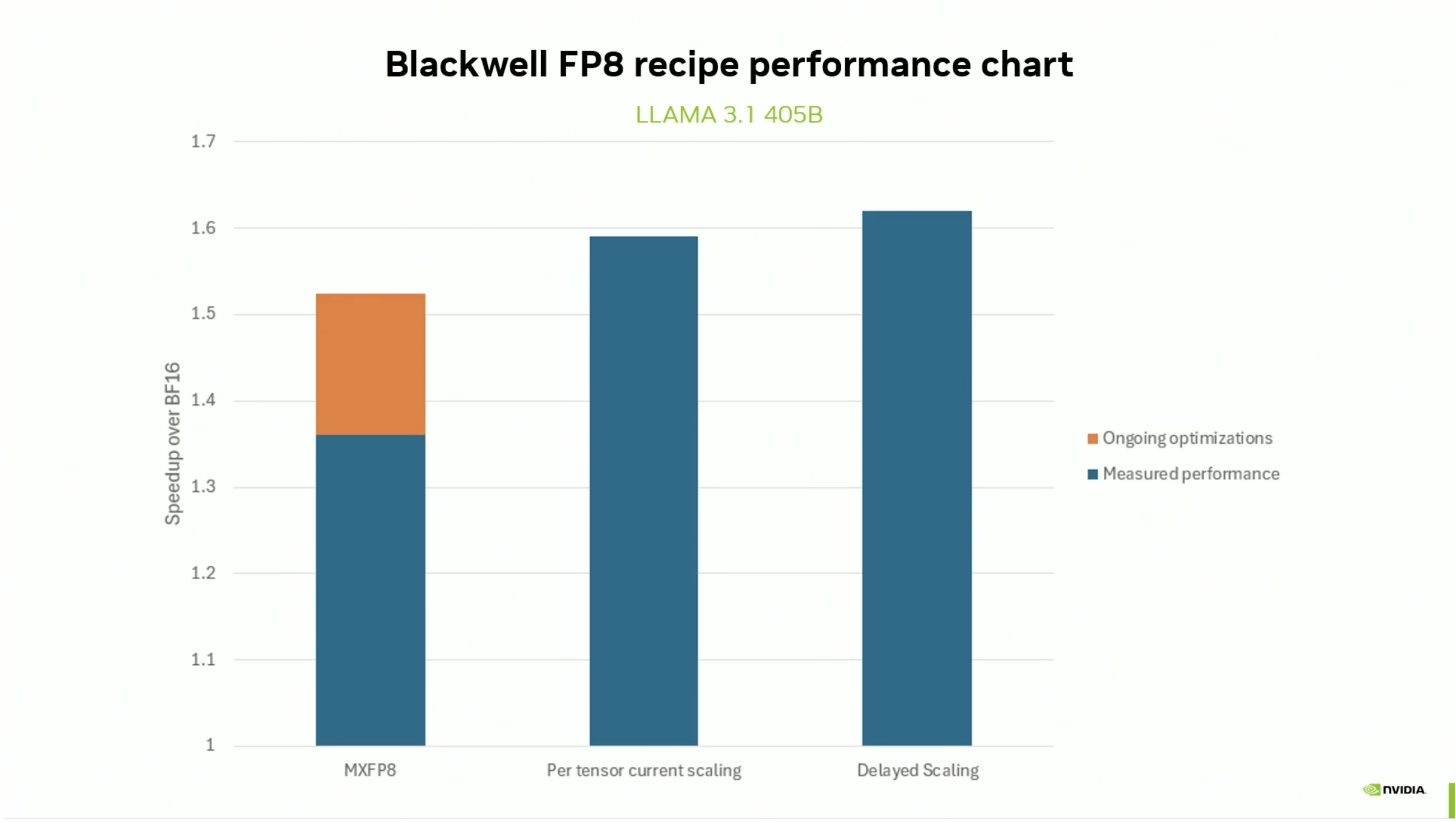
The “MXFP8” bar is a reasonably close analog to the “DSv3 subchannel-wise” bar in the H100 plot and shows that it should be possible to get a 50%-60% speedup over training in BF16 by using Blackwell and the right FP8 recipe.
This left me wondering, though: why in the world would you ever use MXFP8 if it’s so much worse than the other recipes where you apply just one scaling factor to a much coarser block of values such as a whole tensor?
As it turns out, you don’t use MXFP8 because you can, you use it because you have to. When training in FP8, you have to carefully watch for signs of numerical instability—the loss function starting to go crazy, gradient norms jumping up or down dramatically, or values saturating at their precision limits and underflowing or overflowing, resulting in NaNs or Infs everywhere.
So, from what I can tell, actually training in FP8 looks something like this:
- You start by partitioning the model into FP8-safe, FP16-safe, and unsafe regions using as coarse of a granularity of scaling factors as possible to achieve the highest speedup over training only in FP16.
- You train until you start seeing numerical instabilities arising. Then you have to stop training and rewind a bit to undo the damage done by all the overflows and underflows.
- You re-train from an older checkpoint using higher precision to see if your instability goes away. If the instability doesn’t occur when using high precision, you know your problem was the result of the dynamic range in your FP8 regions getting too big.
- Switch those FP8 regions with high dynamic range into finer-grained MXFP8 format and resume training. It will be slower than before since MXFP8 isn’t as fast as coarser-grained FP8, but hopefully the numerical instability doesn’t come back.
I think Transformer Engine helps with steps 1 and 4, but I think steps 2 and 3 require some degree of artistry or slick automation.
4-bit precision
NVIDIA announced that they trained a 12B parameter Mamba+Transformer model using NVFP4 in 2025.1 They showed that training in NVP4 instead of FP8 shows the same learning rate (e.g., doesn’t require more training tokens) and same quality (via model benchmarks). They did not disclose the end-to-end speedup that training in NVFP4 offers, though.